Appendix (Reference Topics)

Appendix (Reference Topics)

Slides

This module is also available in the following versions

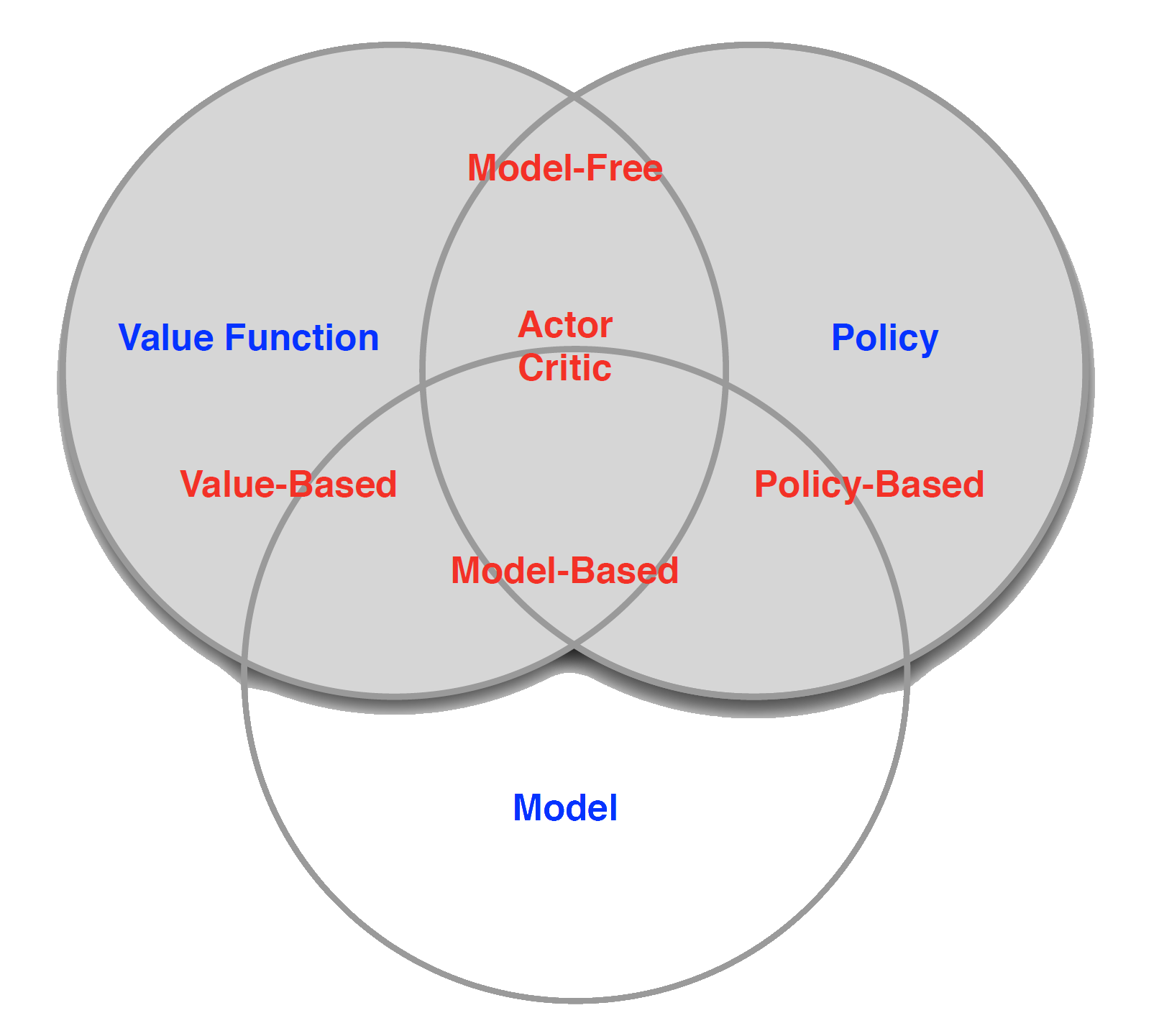
Categorizing agents

Value Based

  • No Policy (Implicit)

  • Value Function

Policy Based

  • Policy

  • No Value Function

Actor Critic

  • Policy
  • Value Function

Categorizing agents (continued)

Model Free

  • Policy and/or Value Function

  • No Model

Model Based

  • Policy and/or Value Function

  • Model

Example Taxonomy

Computational Complexity of Planning

Algorithmic Problems in Planning

Satisficing Planning

Input: A planning task \(P\).
Output: A plan for \(P\), or unsolvable if no plan for \(P\) exists.

Optimal Planning

Input: A planning task \(P\).
Output: An optimal plan for \(P\), or unsolvable if no plan for \(P\) exists.

\(\rightarrow\) The techniques successful for either one of these are almost disjoint!

\(\rightarrow\) Satisficing planning is much more effective in practice

\(\rightarrow\) Programs solving these problems are called planners, planning systems, or planning tools.

Decision Problems in Planning

Definition (PlanEx). By PlanEx, we denote the problem of deciding, given a planning task \(P\), whether or not there exists a plan for \(P\).

\(\rightarrow\) Corresponds to satisficing planning.

 

Definition (PlanLen). By PlanLen, we denote the problem of deciding, given a planning task \(P\) and an integer \(B\), whether or not there exists a plan for \(P\) of length at most \(B\).

\(\rightarrow\) Corresponds to optimal planning.

NP & PSPACE Classes (Refresher)

NP: Decision problems for which there exists a non-deterministic Turing machine that runs in time polynomial in the size of its input.

  • Accepts if at least one of the possible runs accepts.

PSPACE: Decision problems for which there exists a deterministic Turing machine that runs in space polynomial in the size of its input.

 

Relationship between classes: Non-deterministic polynomial space can be simulated in deterministic polynomial space.

  • Thus PSPACE = NPSPACE, and hence (trivially) NP \(\subset\) PSPACE.

For details see a computational complexity textbook, such as Garey and Johnson (1979).

Computational Complexity of PlanEx and PlanLen

Theorem. PlanEx and PlanLen are PSPACE-complete.

  • “At least as hard as any other problem contained in PSPACE.”
  • Details: Bylander (1994).

Domain-Specific PlanEx vs. PlanLen

  • In general, both have the same complexity.
  • Within particular applications, bounded length plan existence is often harder than plan existence.
  • This happens in many IPC benchmark domains: PlanLen is NP-complete while PlanEx is in P.
    • For example: Blocksworld and Logistics.
  • In practice, optimal planning is (almost) never “easy”.

Is Blocksworld Hard?

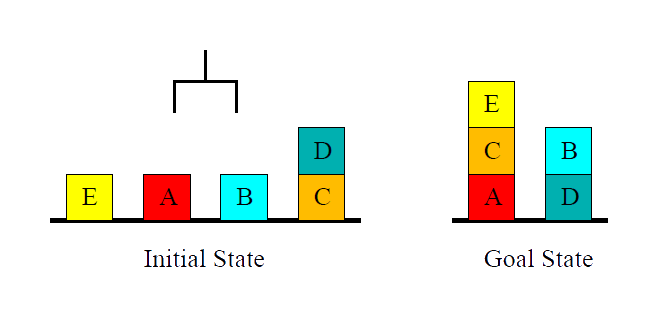
Blocksworld is Hard!

Why All the Fuss? Example Blocksworld

  • \(n\) blocks, \(1\) hand.
  • A single action either takes a block with the hand or puts a block we’re holding onto some other block/the table.

State Space Growth in Blocksworld

blocks states
1 1
2 3
3 13
4 73
5 501
6 4051
7 37633
8 394353 …
blocks states
9 4596553
10 58941091
11 824073141
12 12470162233
13 202976401213
14 3535017524403
15 65573803186921
16 1290434218669921

\(\rightarrow\) State spaces may be huge. In particular, the state space is typically exponentially large in the size of its specification via the problem \(\Pi\) (up next).

\(\rightarrow\) In other words: search problems typically are computationally hard (e.g., optimal Blocksworld solving is NP-complete).

Convergence & Contraction Mapping Theorem

Convergence?

How do we know that value iteration converges to \(v_*\)?

Or that iterative policy evaluation converges to \(v_{\pi}\)?

And therefore that policy iteration converges to \(v_*\)?

Is the solution unique?

How fast do these algorithms converge?

These questions are resolved by contraction mapping theorem

Value Function Space

Consider the vector space \(\mathcal{V}\) over value functions

  • There are \(|\mathcal{S}|\) dimensions

  • Each point in this space fully specifies a value function \(v(s)\)

What does a Bellman backup do to points in this space?

  • We will show that it brings value functions closer,

  • \(\ldots\) and therefore the backups must converge on a unique solution

Value Function \(\infty\)-Norm

We will measure distance between state-value functions \(u\) and \(v\) by the \(\infty\)-norm

i.e. the largest difference between state values,

\[ \|u - v\|_{\infty} = \max_{s \in \mathcal{S}} |u(s) - v(s)| \]

Bellman Expectation Backup is a Contraction

Define the Bellman expectation backup operator \(T^{\pi}\)

\[ T^{\pi}(v) = \mathcal{R}^{\pi} + \gamma \mathcal{P}^{\pi} v \]

This operator is a \(\gamma\)-contraction, i.e. it makes value functions closer by at least \(\gamma\):

\[ \begin{align*} \|T^{\pi}(u) - T^{\pi}(v)\|_{\infty} &= \|(\mathcal{R}^{\pi} + \gamma \mathcal{P}^{\pi} u) - (\mathcal{R}^{\pi} + \gamma \mathcal{P}^{\pi} v)\|_{\infty} \\[4pt] &= \|\gamma \mathcal{P}^{\pi} (u - v)\|_{\infty} \\[4pt] &\le \|\gamma \mathcal{P}^{\pi}\|_{\infty} \, \|u - v\|_{\infty} \\[4pt] &\le \gamma \, \|u - v\|_{\infty} \end{align*} \]

Contraction Mapping Theorem

Theorem (Contraction Mapping Theorem)

For any metric space \(\mathcal{V}\) that is complete (i.e. closed) under an operator \(T(v)\), where \(T\) is a \(\gamma\)-contraction,

  • \(T\) converges to a unique fixed point

  • At a linear convergence rate of \(\gamma\)

Convergence of Policy Evaluation and Policy Iteration

The Bellman expectation operator \(T^{\pi}\) has a unique fixed point

\(v_{\pi}\) is a fixed point of \(T^{\pi}\) (by the Bellman expectation equation)

By the contraction mapping theorem

Iterative policy evaluation converges on \(v_{\pi}\)

Policy iteration converges on \(v_{*}\)

Bellman Optimality Backup is a Contraction

Define the Bellman optimality backup operator \(T^{*}\),

\[ T^{*}(v) = \max_{a \in \mathcal{A}} \left( \mathcal{R}^{a} + \gamma \mathcal{P}^{a} v \right) \]

This operator is a \(\gamma\)-contraction,
i.e. it makes value functions closer by at least \(\gamma\)
(similar to previous proof)

\[ \|T^{*}(u) - T^{*}(v)\|_{\infty} \le \gamma \|u - v\|_{\infty} \]

Convergence of Value Iteration

The Bellman optimality operator \(T^*\) has a unique fixed point

\(v_*\) is a fixed point of \(T^*\) (by Bellman optimality equation)

By contraction mapping theorem

Value iteration converges on \(v_*\)

Relationship Between Forward and Backward TD

TD(\(\lambda\)) and TD(\(0\))

When \(\lambda = 0\), only the current state is updated

\[ \begin{align*} E_t(s) & = \mathbf{1}(S_t = s)\\[0pt] V(s) & \leftarrow V(s) + \alpha \delta_t E_t(s) \end{align*} \]

This is exactly equivalent to the TD(\(0\)) update

\[ V(S_t) \leftarrow V(S_t) + \alpha \delta_t \]

TD(\(\lambda\)) and MC(\(0\))

When \(\lambda = 1\), credit is deferred until the end of the episode

  • Consider episodic environments with offline updates

  • Over the course of an episode, total update for TD(\(1\)) is the same as total update for MC

Theorem

The sum of offline updates is identical for forward-view and backward-view TD(\(\lambda\))

\[ \sum_{t=1}^{T} \alpha \delta_t E_t(s) = \sum_{t=1}^{T} \alpha \left( G_t^{\lambda} - V(S_t) \right) \mathbf{1}(S_t = s) \]

MC and TD(\(1\))

Consider an episode where \(s\) is visited once at time-step \(k\)

  • TD(1) eligibility trace discounts time since visit:

\[ \begin{align*} E_t(s) & = \gamma E_{t-1}(s) + \mathbf{1}(S_t = s)\\[0pt] & = \begin{cases} 0, & \text{if } t < k \\ \gamma^{t-k}, & \text{if } t \ge k \end{cases} \end{align*} \]

  • TD(1) updates accumulate error online:

\[ \sum_{t=1}^{T-1} \alpha \delta_t E_t(s) = \alpha \sum_{t=k}^{T-1} \gamma^{t-k} \delta_t = \alpha (G_k - V(S_k)) \]

  • By the end of the episode, it accumulates total error:

\[ \delta_k + \gamma \delta_{k+1} + \gamma^2 \delta_{k+2} + \dots + \gamma^{T-1-k} \delta_{T-1} \]

Telescoping in TD(\(1\))

When \(\lambda = 1\), the sum of TD errors telescopes into the Monte Carlo (MC) error:

\[ \begin{align*} & \delta_t + \gamma \delta_{t+1} + \gamma^{2}\delta_{t+2} + \dots + \gamma^{T-1-t}\delta_{T-1}\\[0pt] & =\; R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\\[0pt] & +\; \gamma R_{t+2} + \gamma^{2} V(S_{t+2}) - \gamma V(S_{t+1})\\[0pt] & +\; \gamma^{2} R_{t+3} + \gamma^{3} V(S_{t+3}) - \gamma^{2} V(S_{t+2})\\[0pt] & \quad \quad \quad \vdots\\[0pt] & +\; \gamma^{T-1-t} R_T + \gamma^{T-t} V(S_T) - \gamma^{T-1-t} V(S_{T-1})\\[0pt] & =\; R_{t+1} + \gamma R_{t+2} + \gamma^{2} R_{t+3} + \dots + \gamma^{T-1-t} R_T - V(S_t)\\[0pt] & =\; G_t - V(S_t) \end{align*} \]

TD(\(\lambda\)) and TD(\(1\))

TD(\(1\)) is roughly equivalent to every-visit Monte-Carlo

Error is accumulated online, step-by-step

If value function is only updated online at end of episode

Then total update is exactly the same as MC

Telescoping in TD(\(\lambda\))

For general \(\lambda\), TD errors also telescope to the \(\lambda\)-error, \(G_t^{\lambda} - V(S_t)\)

\[ \begin{align*} & G_t^{\lambda}-V(S_t)\hspace{-15mm} &=-V(S_t) &+(1-\lambda)\lambda^{0}(R_{t+1} + \gamma V(S_{t+1}))\\[0pt] & & &+(1-\lambda)\lambda^{1}(R_{t+1}+\gamma R_{t+2}+\gamma^{2} V(S_{t+2})) \\[0pt] & & & + (1 - \lambda)\lambda^{2}(R_{t+1} + \gamma R_{t+2} + \gamma^{2} R_{t+3} + \gamma^{3} V(S_{t+3}))\\[0pt] & & &+ \dots \\[0pt] & &= -V(S_t) &+(\gamma\lambda)^{0}(R_{t+1}+\gamma V(S_{t+1})-\gamma\lambda V(S_{t+1})) \\[0pt] & & & + (\gamma\lambda)^{1}(R_{t+2} + \gamma V(S_{t+2}) - \gamma\lambda V(S_{t+2})) \\[0pt] & & & + (\gamma\lambda)^{2}(R_{t+3} + \gamma V(S_{t+3}) - \gamma\lambda V(S_{t+3})) \\[0pt] & & & + \dots \\[0pt] & &= \quad \quad \quad \quad & \quad (\gamma\lambda)^{0}(R_{t+1} + \gamma V(S_{t+1}) - V(S_t)) \\[0pt] & & & + (\gamma\lambda)^{1}(R_{t+2} + \gamma V(S_{t+2}) - V(S_{t+1})) \\[0pt] & & & + (\gamma\lambda)^{2}(R_{t+3} + \gamma V(S_{t+3}) - V(S_{t+2})) \\[0pt] & & & + \dots \\[0pt] & & & \hspace{-37mm} = \delta_t + \gamma\lambda \delta_{t+1} + (\gamma\lambda)^2 \delta_{t+2} + \dots \end{align*} \]

Forwards and Backwards TD(\(\lambda\))

Consider an episode where \(s\) is visited once at time-step \(k\)

TD(\(\lambda\)) eligibility trace discounts time since visit:

\[ \begin{align*} E_t(s) & = \gamma \lambda E_{t-1}(s) + \mathbf{1}(S_t = s)\\[0pt] & = \begin{cases} 0, & \text{if } t < k \\ (\gamma \lambda)^{t-k}, & \text{if } t \ge k \end{cases} \end{align*} \]

Backward TD(\(\lambda\)) updates accumulate error online:

\[ \sum_{t=1}^{T} \alpha \delta_t E_t(s) = \alpha \sum_{t=k}^{T} (\gamma \lambda)^{t-k} \delta_t = \alpha \left(G_k^{\lambda} - V(S_k)\right) \]

  • By the end of the episode, it accumulates total error for the \(\lambda\)-return

  • For multiple visits to \(s\), \(E_t(s)\) accumulates many errors

Offline Equivalence of Forward and Backward TD

Offline updates

  • Updates are accumulated within episode

  • but applied in batch at the end of episode

Online Equivalence of Forward and Backward TD

Online updates

  • TD(\(\lambda\)) updates are applied online at each step within episode

  • Forward and backward-view TD(\(\lambda\)) are slightly different

  • Exact online TD(\(\lambda\)) achieves perfect equivalence

  • By using a slightly different form of eligibility trace


Harm van Seijen, A. Rupam Mahmood, Patrick M. Pilarski, Marlos C. Machado, Richard S. Sutton; True Online Temporal-Difference Learning. Journal of Machine Learning Research (JMLR), 17(145):1−40, 2016.

Summary of Forward and Backward TD(\(\lambda\))

\[ \begin{array}{|c|c|c|c|} \hline {\color{red}{\text{Offline updates}}} & {\color{red}{\lambda = 0}} & {\color{red}{\lambda \in (0,1)}} & {\color{red}{\lambda = 1}} \\ \hline \text{Backward view} & \text{TD(0)} & \text{TD}(\lambda) & \text{TD(1)} \\[0pt] & || & || & || \\[0pt] \text{Forward view} & \text{TD(0)} & \text{Forward TD}(\lambda) & \text{MC} \\[0pt] \hline {\color{red}{\text{Online updates}}} & {\color{red}{\lambda = 0}} & {\color{red}{\lambda \in (0,1)}} & {\color{red}{\lambda = 1}} \\ \hline \text{Backward view} & \text{TD(0)} & \text{TD}(\lambda) & \text{TD(1)} \\[0pt] & || & \neq & \neq \\[0pt] \text{Forward view} & \text{TD(0)} & \text{Forward TD}(\lambda) & \text{MC} \\[0pt] & || & || & || \\[0pt] \text{Exact Online} & \text{TD(0)} & \text{Exact Online TD}(\lambda) & \text{Exact Online TD(1)} \\ \hline \end{array} \]

= here indicates equivalence in total update at end of episode.

Linear Least Squares Methods

Linear Least Squares Prediction

Experience replay finds the least squares solution

  • But may take many iterations.

Using the special case of linear value function approximation

\[ \hat{v}(s,\mathbf{w}) = x(s)^\top \mathbf{w} \]

We can solve the least squares solution directly using a closed form

Linear Least Squares Prediction (2)

At the minimum of \(LS(\mathbf{w})\), the expected update must be zero:

\[\begin{align*} \mathbb{E}_{\mathcal{D}} \left[ \Delta \mathbf{w} \right] &= 0\;\;\; \text{(want update zero across data set)} \\[0pt] \alpha \sum_{t=1}^{T} \mathbf{x}(s_t) \bigl( v_t^{\pi} - \mathbf{x}(s_t)^{\top} \mathbf{w} \bigr) &= 0\;\;\; \text{(unwrapping expected updates)}\\[0pt] \sum_{t=1}^{T} \mathbf{x}(s_t) v_t^{\pi} &= \sum_{t=1}^{T} \mathbf{x}(s_t) \mathbf{x}(s_t)^{\top} \mathbf{w} \\[0pt] \mathbf{w} &= \left( \sum_{t=1}^{T} \mathbf{x}(s_t) \mathbf{x}(s_t)^{\top} \right)^{-1} \sum_{t=1}^{T} \mathbf{x}(s_t) v_t^{\pi} \end{align*}\]

Compute time: \(O(N^3)\) for \(N\) features (direct),
or incremental \(O(N^2)\) using Sherman–Morrison.

  • Sometimes better or cheaper than experience replay, e.g. if have only a few features for the linear cases.

Linear Least Squares Prediction Algorithms

We do not know true values \(v_t^\pi\)

  • In practice, our “training data” must use noisy or biased samples of \(v^{\pi}_t\)

\[\begin{align*} {\color{blue}{\text{LSMC}}} \;\;\;\;&\text{Least Squares Monte-Carlo uses return}\\[0pt] & v_t^\pi \approx {\color{red}{G_t}} \\[0pt] {\color{blue}{\text {LSTD}}} \;\;\;\; & \text{Least Squares Temporal-Difference uses TD target}\\[0pt] & v_t^\pi \approx {\color{red}{R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w})}}\\[0pt] {\color{blue}{\text{LSTD}}}{\color{blue}{(\lambda)}}\;\;\;\; & \text{Least Squares TD}(\lambda)\text{ uses}\;\lambda\text{-return} \\[0pt] & v_t^\pi \approx {\color{red}{G_t^\lambda}} \end{align*}\]

In each case we can solve directly for the fixed point of MC / TD / TD(\(\lambda\))

Linear Least Squares Prediction Algorithms (2)

\[\begin{align*} {\color{red}{\text{LSMC}}} \;\;\;\; 0 & = \sum_{t=1}^T \alpha \big(G_t - \hat{v}(S_t,\mathbf{w})\big)\, \textbf{x}(S_t),\qquad\\[0pt] \mathbf{w} & = \left(\sum_{t=1}^T \textbf{x}(S_t) \textbf{x}(S_t)^\top \right)^{-1} \left(\sum_{t=1}^T \textbf{x}(S_t) G_t \right)\\[0pt] {\color{red}{\text{LSTD}}} \;\;\;\; 0 & = \sum_{t=1}^T \alpha \big(R_{t+1} + \gamma \hat{v}(S_{t+1},\mathbf{w}) - \hat{v}(S_t,\mathbf{w})\big)\, \textbf{x}(S_t)\\[0pt] \mathbf{w} & = \left(\sum_{t=1}^T \textbf{x}(S_t)\big(x(S_t) - \gamma \textbf{x}(S_{t+1})\big)^\top \right)^{-1} \left(\sum_{t=1}^T \textbf{x}(S_t) R_{t+1}\right)\\[0pt] {\color{red}{\text{LSTD}}}{\color{red}{(\lambda)}}\;\;\;\; 0 & = \sum_{t=1}^T \alpha\, \delta_t\, E_t,\qquad\\[0pt] \mathbf{w} & = \left(\sum_{t=1}^T E_t \big(\textbf{x}(S_t) - \gamma \textbf{x}(S_{t+1})\big)^\top \right)^{-1} \left(\sum_{t=1}^T E_t R_{t+1}\right) \end{align*}\]

Convergence of Linear Least Squares Prediction Algorithms

\[ \begin{array}{l l c c c} \hline \text{On/Off-Policy} & \text{Algorithm} & \text{Table Lookup} & \text{Linear} & \text{Non-Linear} \\ \hline \text{On-Policy} & \textit{MC} & \checkmark & \checkmark & \checkmark \\ & {\color{red}{\textit{LSMC}}} & {\color{red}{\checkmark}} & {\color{red}{\checkmark}} & {\color{red}{-}} \\ & \textit{TD} & \checkmark & \checkmark & \text{✗} \\ & {\color{red}{\textit{LSTD}}} & {\color{red}{\checkmark}} & {\color{red}{\checkmark}} & {\color{red}{-}} \\ \hline \text{Off-Policy} & \textit{MC} & \checkmark & \checkmark & \checkmark \\ & {\color{red}{\textit{LSMC}}} & {\color{red}{\checkmark}} & {\color{red}{\checkmark}} & {\color{red}{-}} \\ & \textit{TD} & \checkmark & \text{✗} & \text{✗} \\ & {\color{red}{\textit{LSTD}}} & {\color{red}{\checkmark}} & {\color{red}{\checkmark}} & {\color{red}{-}} \\ \hline \end{array} \]

Least Squares Policy Iteration

Policy evaluation Policy evaluation by least-squares Q-learning

Policy improvement Greedy policy improvement

Least Squares Action-Value Function Approximation

Approximate action-value function \(q_\pi(s, a)\)

  • using linear combination of features \(\mathbf{x}(s, a)\)

\[ \hat{q}(s, a, \mathbf{w}) = \mathbf{x}(s, a)^\top \mathbf{w} \;\approx\; q_\pi(s, a) \]

Minimise least squares error between \(\hat{q}(s, a, \mathbf{w})\) and \(q_\pi(s, a)\)

  • from experience generated using policy \(\pi\)

  • consisting of \(\langle (state, action), value \rangle\) pairs

\[ \mathcal{D} = \Bigl\{ \langle (s_1, a_1), v_1^\pi \rangle,\; \langle (s_2, a_2), v_2^\pi \rangle,\; \ldots,\; \langle (s_T, a_T), v_T^\pi \rangle \Bigr\} \]

Least Squares Control

For policy evaluation, we want to efficiently use all experience

For control, we also want to improve the policy

The experience is generated from many policies

So to evaluate \(q_\pi(S,A)\) we must learn off-policy

We use the same idea as Q-learning:

  • Experience from old policy: \((S_t, A_t, R_{t+1}, S_{t+1}) \sim \pi_{\text{old}}\)
  • Consider alternative successor action \(A^{\prime} = \pi_{\text{new}}(S_{t+1})\)
  • Update \(\hat{q}(S_t, A_t, \mathbf{w})\) toward
    \[ R_{t+1} + \gamma\, \hat{q}(S_{t+1}, A^{\prime}, \mathbf{w}) \]

Least Squares Q-Learning

Consider the following linear Q-learning update

\[\begin{align*} \delta &= R_{t+1} + \gamma \hat{q}(S_{t+1}, {\color{red}{\pi(S_{t+1})}}, \mathbf{w}) - \hat{q}(S_t, A_t, \mathbf{w}) \\[0.5em] \Delta \mathbf{w} &= \alpha \, \delta \, \mathbf{x}(S_t, A_t) \end{align*}\]

LSTDQ algorithm: solve for total update \(=\) zero

\[\begin{align*} 0 &= \sum_{t=1}^T \alpha \Big( R_{t+1} + \gamma \hat{q}(S_{t+1}, {\color{red}{\pi(S_{t+1})}}, \mathbf{w}) - \hat{q}(S_t, A_t, \mathbf{w}) \Big)\mathbf{x}(S_t, A_t) \\[1em] \mathbf{w} &= \Bigg( \sum_{t=1}^T \mathbf{x}(S_t, A_t)\big(\mathbf{x}(S_t, A_t) - \gamma \mathbf{x}(S_{t+1}, \pi(S_{t+1}))\big)^\top \Bigg)^{-1} \sum_{t=1}^T \mathbf{x}(S_t, A_t) R_{t+1} \end{align*}\]

Least Squares Policy Iteration Algorithm

The following pseudo-code uses LSTDQ for policy evaluation

It repeatedly re-evaluates experience \(\mathcal{D}\) with different policies

Least Squares Policy Iteration Algorithm (LSTFQ variant)

\[ \begin{aligned} &\text{function LSPI-TD}(\mathcal{D}, \pi_0) \\ &\quad \pi^{\prime} \leftarrow \pi_0 \\ &\quad \text{repeat} \\ &\qquad \pi \leftarrow \pi^{\prime} \\ &\qquad Q \leftarrow \text{LSTDQ}(\pi,\mathcal{D}) \\ &\qquad \text{for all } s \in S \text{ do} \\ &\qquad\quad \pi^{\prime}(s) \leftarrow \arg\max_{a \in A} Q(s,a) \\ &\qquad \text{end for} \\ &\quad \text{until } (\pi \approx \pi^{\prime}) \\ &\quad \text{return } \pi \\ &\text{end function} \end{aligned} \]

Convergence of Control Algorithms

\[ \begin{array}{l l c c c} \hline \text{Algorithm} & \text{Table Lookup} & \text{Linear} & \text{Non-Linear} \\ \hline \textit{Monte-Carlo Control} & \checkmark & (\checkmark) & \text{✗} \\ \textit{Sarsa} & \checkmark & (\checkmark) & \text{✗} \\ \textit{Q-Learning} & \checkmark & \text{✗} & \text{✗} \\ \textit{\color{red}{LSPI}} & \checkmark & (\checkmark) & - \\ \hline \end{array} \]

(\(\checkmark\)) = chatters around near-optimal value function.

Chain Walk Example (More complicated random walk)

Consider the 50 state version of this problem (bigger replica of this diagram)

  • Reward \(+1\) in states \(10\) and \(41\), \(0\) elsewhere

  • Optimal policy: R (\(1-9\)), L (\(10-25\)), R (\(26-41\)), L (\(42, 50\))

  • Features: \(10\) evenly spaced Gaussians (\(\sigma = 4\)) for each action

  • Experience: \(10,000\) steps from random walk policy

LSPI in Chain Walk: Action-Value Function

Plots show LSPI iterations on a 50-state chain with a radial basis function approximator.

  • The colours represent two different actions of going left (blue) or right (red)

  • The plots show the true value function (dashed) or approximate value function

  • You can see it converges to the optimal policy after only \(7\) iterations.

LSPI in Chain Walk: Policy

Plots of policy improvement over LSPI iterations (using same 50-state chain example).

  • Shows convergence of LSPI policy to optimal within a few iterations.

Natural Actor-Critic (Advanced Topic)

Alternative Policy Gradient Directions


Gradient ascent algorithms can follow any ascent direction

  • A good ascent direction can significantly speed convergence

Also, a policy can often be reparametrised without changing action probabilities

  • For example, increasing score of all actions in a softmax policy

  • The vanilla gradient is sensitive to these reparametrisations

Compatible Function Approximation (CFA)

Policy Gradient with a Learned Critic

We want to estimate the true gradient \[ \nabla_\theta J(\theta) = \mathbb{E}_\pi \!\left[ \nabla_\theta \log \pi_\theta(a|s)\, Q^\pi(s,a) \right] \]

But \(Q^\pi(s,a)\) is unknown — so we approximate it with a parametric critic \({\color{red}{Q_w(s,a)}}\)

Compatibility Conditions for Critic

  1. Linear in the policy’s score function \[ Q_w(s,a) = w^\top \nabla_\theta \log \pi_\theta(a|s) \]

  2. Weights chosen to minimise on-policy error \[ w^* = \arg\min_w \mathbb{E}_\pi \left[ \big(Q^\pi(s,a) - Q_w(s,a)\big)^2 \right] \]

Compatibility Conditions—A Beautiful Result

If both compatibility conditions hold, then

\[ \nabla_\theta J(\theta) = \mathbb{E}_\pi \left[ \nabla_\theta \log \pi_\theta(a|s)\, Q_w(s,a) \right] \]

That is — the approximate critic yields the exact policy gradient.

Intuition

  • The critic lies in the same space as the policy’s gradient features

  • The actor and critic share a common geometry

  • The critic projects \(Q^\pi\) onto the policy’s tangent space

  • Variance reduction without bias — a perfect harmony between learning and estimation

Natural Policy Gradient—Fisher Information Matrix

The natural policy gradient is parametrisation independent

  • It finds the ascent direction that is closest to the vanilla gradient, when changing policy by a small, fixed amount

\[ \nabla^{\text{nat}}_{\theta} \pi_{\theta}(s,a) = G_{\theta}^{-1} \nabla_{\theta} \pi_{\theta}(s,a) \]

  • where \(G_{\theta}\) is the Fisher information matrix (Measures how sensitive a probability distribution is to changes in its parameters) \[ G_{\theta} = \mathbb{E}_{\pi_{\theta}} \Big[ {\color{blue}{\nabla_{\theta} \log \pi_{\theta}(s,a) \; \nabla_{\theta} \log \pi_{\theta}(s,a)^\top }}\Big] \]

Natural Actor-Critic—Compatible Function Approximation

Uses compatible function approximation,

\[ \nabla_{\mathbf{w}} A_{\mathbf{w}}(s,a) = \nabla_{\theta} \log \pi_{\theta}(s,a) \]

So the natural policy gradient simplifies,

\[ \begin{align*} \nabla_{\theta} J(\theta) &= \mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a) \; A^{\pi_{\theta}}(s,a) \big] \\[2pt] &= \mathbb{E}_{\pi_{\theta}} \Big[ \nabla_{\theta} \log \pi_{theta}(s,a) \, \nabla_{\theta} \log \pi_{\theta}(s,a)^\top \Big] \mathbf{w} \\[2pt] &= G_{\theta} \, \mathbf{w}\\[2pt] {\color{red}{\nabla_{\theta}^{\text{nat}} J(\theta)}} & {\color{red}{= \mathbf{w}}} \end{align*} \]

i.e. update actor parameters in direction of critic parameters \(\mathbf{w}\)

Natural Policy Gradient—Parameterisation Invariant

  • The black contours show level sets of equal performance \(J(\theta)\)
  • The blue arrows show the ordinary gradient ascent direction for each point in parameter space (not orthogonal to the contours, behave irregularly across space)
  • The red arrows are the natural gradient directions (ascent directions are orthogonal to contours and smoothly distributed)
  • Natural gradient respects geometry of probability distributions—it finds steepest ascent direction measured in policy (distributional) space, not raw parameter space

Natural Actor Critic in Snake Domain

  • The dynamics are nonlinear and continuous—a good test of policy gradient methods.

Natural Actor Critic in Snake Domain (2)

  • The geometry of the corridor causes simple gradient updates to oscillate or diverge, but natural gradients (which adapt to curvature via the Fisher matrix independent of parameters) make stable, efficient progress.

Proximal Policy Optimisation (PPO) (Advanced Topic)

Proximal Policy Optimisation (PPO)


Goal: Stable, sample-efficient policy improvement

Idea: Constrain how far the new policy moves from the old one at each update during actor-critic cycle

Policy Objective Functions (Revisited)

From a policy gradient perspective, the true objective function \(J^{{\pi}_{\theta}}(\theta)\) over policy \(\pi_{\theta}\) is defined as follows

\[ J^{{\pi}_{\theta}}(\theta) = \mathbb{E}_{\tau \sim \pi_{\theta}} [G_0]=V^{\pi \theta}(d_0) \]

where \(d_0\) is the distribution over initial states at the start of each episode \(\tau\)

However, there are two problems in the actor-critic setting:

1. Computing \(J^{{\pi}_{\theta}}(\theta)\) exactly would require integrating over all trajectories, \(\tau\), of the current policy, which is impractical

2. If we update the parameters \(\theta\), it will effect objective value during the optimisation process, leading to (circular) feedback

We therefore need a surrogate objective independent of the trajectory distribution under the new policy \(\color{blue}{\pi_{\theta}}\) we are building

Surrogate Objective

From the policy-gradient theorem, we can define the importance ratio

\[ r_t(\theta) \;=\; \frac{\pi_\theta(a_t\mid s_t)}{\pi_{\theta_{\text{old}}}(a_t\mid s_t)} \qquad \]

We now define the surrogate objective \(L_{PG}\) for the true objective

\[ L_{PG}(\theta) \;=\; \mathbb{E}_t\!\big[\, r_t(\theta)\,\hat A_t \,\big] \]

  • Where \(\hat{A}_t\) captures how much better action \(a_t\) was than the state’s average

  • \(\hat{A}_t\) is an estimator of the true advantage function \(A^{\pi}\)

  • \(A^{\pi}(s_t,a_t) = Q^{\pi}(s_t, a_t) - V^{\pi}(S_t)\)

Clipped Surrogate (Core Idea)

Kullback-Leibler (KL) divergence theory tells us we want improvement without overly large steps in policy space, so we define

\[ L^{\text{CLIP}}(\theta) \;=\; \mathbb{E}_t\! \left[ \min\!\Big( r_t(\theta)\,\hat A_t,\; \mathrm{clip}\!\big(r_t(\theta),\,1-\epsilon,\,1+\epsilon\big)\,\hat A_t \Big) \right] \]

  • If \(r_t(\theta)\) leaves the interval \([1-\epsilon,\,1+\epsilon]\), the objective is clipped.

  • Typical range for \(\epsilon \in [0.1,\,0.2]\).

  • Prevents destructive updates while preserving ascent direction

The clipped surrogate objective in PPO plays a similar stabilising role to compatible function approximation — both constrain policy updates so that gradient estimates remain accurate and unbiased with respect to the true policy improvement direction.

Complete PPO loss

\[ L^{\text{PPO}}(\theta) = \mathbb{E}_t\!\Big[{\color{blue}{L^{\text{CLIP}}(\theta)}} - c_1\,{\color{red}{\big(V_\theta(s_t)-V_t^{\text{target}}\big)^2}} + c_2\,\mathcal{H}\!\left[\pi_\theta(\cdot\mid s_t)\right] \Big] \] \(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\)where \(c_1, c_2\) are coefficients

The actors policy gradient (surrogate objective) is \(\color{blue}{L^{CLIP}(\theta)}\)

  • This encourages the policy to increase the probability of actions with positive advantage and decrease it for negative ones

The critics value function is \(\color{red}{\big(V_\theta(s_t)-V_t^{\text{target}}\big)^2}\)

  • This trains the network to predict correct returns (mean-squared error).

The entropy bonus \(\mathcal{H}\) encourages exploration

\[ \mathcal{H}\big[\pi_\theta(\cdot \mid s_t)\big] = - \sum_{a} \pi_\theta(a \mid s_t) \log \pi_\theta(a \mid s_t) \]

The entropy term encourages exploration by rewarding stochastic (uncertain) policies.

  • It’s high when the policy is uncertain or “spread out” (exploratory).

  • It’s low when the policy is confident or deterministic.

  • The dot “\(\cdot\)” in \(\pi_{\theta}(\cdot | s_t)\) means over all possible actions, i.e. the vector of probabilities  \(\pi_{\theta}(a_1,s_t), \pi_{\theta}(a_2,s_t), \ldots\)

In practice this maintains stochasticity until policy becomes more confident or deterministic

Generalised Advantage Estimation (GAE)

In practice, PPO uses a low-variance, low-bias estimate of the advantage \(A^\pi(s_t,a_t)\).

TD error: \[ \delta_t \;=\; r_t + \gamma\,V_\phi(s_{t+1}) - V_\phi(s_t) \]

GAE-\(\lambda\): \[ \hat A_t^{(\lambda)} \;=\; \sum_{l=0}^{\infty} (\gamma\lambda)^l\,\delta_{t+l} \;=\; \delta_t + \gamma\lambda\,\delta_{t+1} + (\gamma\lambda)^2\,\delta_{t+2} + \cdots \]

Return/target used for critic \[ \hat V_t^{\text{target}} \;=\; \hat A_t^{(\lambda)} + V_\phi(s_t) \]

  • \(\lambda\in[0,1]\) trades bias \(\leftrightarrow\) variance, typical PPO: \(\gamma \approx 0.99\), \(\lambda \approx 0.95\).

PPO Algorithm

PPO Algorithm

Repeat

\(\;\;\;\) Collect trajectories with \(\pi_{\theta_{\text{old}}}\)

\(\;\;\;\) Compute returns and advantages using GAE-\(\lambda\)

\(\;\;\;\) Optimise \(L^{\text{CLIP}}\) for \(K\) epochs over mini-batches

\(\;\;\;\) Update old params: \(\theta_{\text{old}} \leftarrow \theta\)

Until a stop condition holds (e.g., total timesteps \(\geq T\), or moving-average return \(\geq R_{\text{target}}\), or max iterations reached)

  • Multiple epochs over the same batch are okay because clipping limits drift

Why PPO works (intuition)

First-order solution method

  • No additional constraint solving required which can introduce second-order effects

Trust-region-like behaviour via clipping

  • Optimisation within trust-region involves only taking steps that stay within a region where local approximation is reliable (founded on KL information theory)

Robust across discrete/continuous control

  • Strong baseline performance in practice

PPO Fine tuning ChatGPT & human feedback (Revisited)

  • Proximal policy optimisation (PPO) is used by ChatGPT 3.5

PPO in Agentic AI, Robotics & World Models

PPO is becoming popular again for Agentic AI modes, and is used in

  • Chat GPT’s Operator, and

  • Claude’s Computer Use modes

PPO is also becoming popular for World Models in robotics, and is used in

  • Vision, Language & Action (VSA) attention-based transformers

Recent Policy Optimisation Techniques

ChatGPT4 uses Direct Preference Optimisation (DPO)

DeepSeek’s R1 uses Group Relative Policy Optimization (GRPO)