11 Policy Gradient (Actor Critic)

Introduction

Policy-Based Reinforcement Learning

In the last module we approximated the value or action-value function using parameters \(\theta\),

\[ \begin{align*} V_\theta(s) &\approx V^\pi(s) \\ Q_\theta(s, a) &\approx Q^\pi(s, a) \end{align*} \]

A policy was generated directly from the value function,
e.g. using \(\epsilon\)-greedy.

In this module we will directly parameterise the policy

\[ \textcolor{red}{\pi_\theta(s, a) = P[a \mid s, \theta]} \]

We will focus again on model-free reinforcement learning, and we directly change the probabilities we pick different actions

Value-Based and Policy-Based RL

Value Based

  • Learnt Value Function

  • Implicit policy (e.g. \(\epsilon\)-greedy)

Policy Based

  • No Value Function

  • Learnt Policy

Actor-Critic

  • Learnt Value Function

  • Learnt Policy


Choice of value-function versus policy approximation sometimes depends on which is easier to compute and store according to the application

Advantages of Policy-Based RL

Advantages:

  • Better convergence properties

  • Effective in high-dimensional or continuous action spaces (as don’t need to estimate \(max\) directly, which can be expensive)

  • Can learn stochastic policies

Disadvantages:

  • Typically converges to a local rather than global optimum

  • Evaluating a policy is typically inefficient and high variance

Example: Rock-Paper-Scissors

Two-player game of rock-paper-scissors

  • Scissors beats paper

  • Rock beats scissors

  • Paper beats rock

A deterministic policy is easily exploited

  • A uniform random policy is optimal (i.e. Nash equilibrium), i.e. optimal behaviour is stochastic

Example: Aliased Gridworld

The agent cannot differentiate the grey states (look the same)

Consider features of the following form of state actions pairs (for all \(N, E, S, W\)):

\[ \phi(s, a) = \mathbf{1}(\text{wall to}\;N, \; a = \text{move}\;E) \]

Compare value-based RL, using an approximate value function:

\[ Q_\theta(s, a) = f(\phi(s, a), \theta) \]

To policy-based RL, using a parameterised policy:

\[ \pi_\theta(s, a) = g(\phi(s, a), \theta) \]

Example: Aliased Gridworld (2)

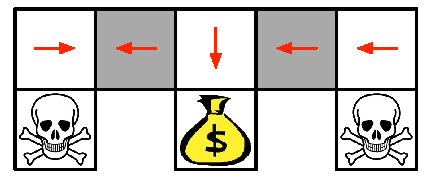
Under aliasing, an optimal deterministic policy will either

  • move \(W\) in both grey states (shown by red arrows)

  • move \(E\) in both grey states

Either way, it can get stuck and never reach the money

Value-based RL learns a near-deterministic policy

  • e.g. greedy or \(\epsilon\)-greedy

So it will traverse the corridor for a long time

Example: Aliased Gridworld (3)

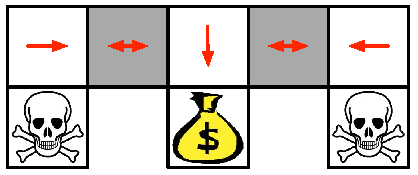
An optimal stochastic policy will randomly move \(E\) or \(W\) in grey states

\[ \begin{align*} \pi_{\theta}(\text{wall to}\;N \text{and}\;S, \text{move}\; E) & = 0:5\\[0pt] \pi_{\theta}(\text{wall to}\;N \text{and}\;S, \text{move}\;W) & = 0:5 \end{align*} \]

It will reach the goal state in a few steps with high probability

Policy-based RL can learn the optimal stochastic policy

Policy Objective Functions

Goal: given policy \(\pi_\theta(s, a)\) with parameters \(\theta\), find best \({\color{blue}{\theta}}\)


But how do we measure the quality of a policy \({\color{blue}{\pi_\theta}}\)?

In episodic environments we can use the start value

\[ J_{1}(\theta) = V^{\pi_\theta}(s_{1}) = \mathbb{E}_{\pi_\theta}[v_{1}] \]

In continuing environments we can use the average value

\[ J_{\text{av}V}(\theta) = \sum_s d^{\pi_\theta}(s) V^{\pi_\theta}(s) \]

Or the average reward per time-step

\[ J_{\text{av}R}(\theta) = \sum_s d^{\pi_\theta}(s) \sum_a \pi_\theta(s, a) R^a_s \]

where \(d^{\pi_\theta}(s)\) is stationary distribution of Markov chain for \(\pi_\theta\)

Policy Optimisation

Policy based reinforcement learning is an optimisation problem

Find \(\theta\) that maximises \(J(\theta)\)

Some optimisation approaches do not use gradient

  • Hill climbing (stochastic—only accepts if an increase, doesn’t compute gradient)

  • Simplex (typically used by e.g. Linear Programming (LP) solvers)

  • Genetic algorithms (stochastic solvers)

Greater efficiency often possible using gradient

  • Gradient descent

  • Conjugate gradient

  • Quasi-newton methods

We focus on gradient descent, many extensions possible

  • And on methods that exploit sequential structure

Finite Difference Policy Gradient

Policy Gradient

Let \(J(\theta)\) be any policy objective function

Policy gradient algorithms search for a local maximum in \(J(\theta)\) by ascending the gradient of the policy, w.r.t. parameters \(\theta\)

\[ \Delta \theta = \alpha \nabla_\theta J(\theta) \]

  • Where \(\nabla_\theta J(\theta)\) is the policy gradient

\[ \nabla_\theta J(\theta) = \begin{pmatrix} \frac{\partial J(\theta)}{\partial \theta_1} \\ \vdots \\ \frac{\partial J(\theta)}{\partial \theta_n} \end{pmatrix} \]

  • and \(\alpha\) is a step-size parameter

Computing Gradients By Finite Differences

To evaluate policy gradient of \(\pi_\theta(s, a)\)
For each dimension \(k \in [1, n]\)

  • Estimate \(k\)th partial derivative of objective function w.r.t. \(\theta\)

  • By perturbing \(\theta\) by small amount \(\epsilon\) in \(k\)th dimension

\[ \frac{\partial J(\theta)}{\partial \theta_k} \;\approx\; \frac{J(\theta + \epsilon u_k) - J(\theta)}{\epsilon} \]

\(\;\;\;\) where \(u_k\) is unit vector with \(1\) in \(k\)th component, \(0\) elsewhere

Uses \(n\) evaluations to compute policy gradient in \(n\) dimensions

  • Simple, noisy, inefficient (might be millions of parameters) – but sometimes effective

  • Works for arbitrary policies, even if policy is not differentiable

Retro Example: Training AIBO to Walk by Finite Difference Policy Gradient

Goal: learn a fast AIBO walk (useful for Robocup)

  • AIBO walk policy is controlled by \(12\) degrees of freedom (elliptical loci)

  • Adapt these parameters by finite difference policy gradient

  • Evaluate performance of policy by field traversal time, 1 degree of freedom at a time

Monte-Carlo Policy Gradient

Score Function

We now compute the policy gradient analytically

  • Assume policy \(\pi_\theta\) is differentiable whenever it is non-zero

  • and we know the gradient \(\nabla_\theta \pi_\theta(s, a)\)

Likelihood ratios exploit the following identity (by rearrangement)

\[ \begin{align*} \nabla_\theta \pi_\theta(s, a) &= \pi_\theta(s, a) \frac{\nabla_\theta \pi_\theta(s, a)}{\pi_\theta(s, a)} \\ &= \pi_\theta(s, a)\nabla_\theta \log \pi_\theta(s, a) \end{align*} \]

The score function is \(\nabla_\theta \log \pi_\theta(s, a)\)

A score function (from machine learning) is the gradient of the log-likelihood with respect to parameters

  • The score function tells you how to adjust policy in a direction to get more of something

  • A large score means that adjusting the parameters in that direction would improve the likelihood of action \(a\)

The score function facilitates easy computation of the expectation

Softmax (Primer)

The softmax function converts a vector of real numbers into a probability distribution.

For a vector of scores: \[ x = [x_1, x_2, \dots, x_n] \]

the softmax is defined as: \[ \text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}} \]

  • Exponentiate each score to make all values positive

  • Normalise them so they sum to 1

  • Produces a smooth (soft) version of the max operation

Example:

\[ x = [2, 1, 0] \quad \Rightarrow \quad e^x = [7.39, 2.72, 1] \]

\[ \text{softmax}(x) = [0.66, 0.24, 0.09] \]

\(\rightarrow\) The highest score gets the largest probability, but all actions still have some chance.

  • Softmax transforms arbitrary real-valued scores into positive, normalised probabilities,

  • allowing us to interpret linear model outputs as stochastic policies.

Softmax Policy

We will use a linear softmax policy as a running example

We first weight actions using linear combination of features \(\phi(s, a)^\top \theta\)

  • Features in Aibo could include position, velocity, distance to goal etc.

  • The probabilities of actions now become proportional to the exponentiated weight

\[ \pi_\theta(s, a) \propto e^{\phi(s,a)^\top \theta} \]

The score function (gradient) is now equivalent to the feature for the action we took minus the average for all the actions:

\[ \begin{align*} \nabla_\theta \log \pi_\theta(s, a) &= \phi(s, a) - \mathbb{E}_{\pi_\theta}[\phi(s, \cdot)] \end{align*} \]

Gaussian Policy

In continuous action spaces, a Gaussian policy is natural to use

  • Mean is a linear combination of state features \(\mu(s) = \phi(s)^\top \theta\)

  • Variance may be fixed \(\sigma^2\), or can also be parameterised

Policy is Gaussian, where actions, \(a\), are sampled from (\(\sim\)) normal distribution \(\mathcal{N}\): \(a \sim \mathcal{N}(\mu(s), \sigma^2)\)

The score function in this case is action minus mean (how much more doing action \(a\)) multiplied by feature, scaled by the variance:

\[ \nabla_\theta \log \pi_\theta(s, a) = \frac{(a - \mu(s))\phi(s)}{\sigma^2} \]

One-Step MDPs

Consider a simple class of one-step MDPs for clarity of explanation

  • Starting in state \(s \sim d(s)\) (select from initial state distribution)

  • Terminating after one time-step with reward \(r = \mathcal{R}_{s,a}\)

Use likelihood ratios to compute the policy gradient

\[ \begin{align*} J(\theta) &= \mathbb{E}_{\pi_\theta}[r] \\ &= \sum_{s \in \mathcal{S}} d(s) \sum_{a \in \mathcal{A}} \pi_\theta(s, a) \mathcal{R}_{s,a} \\ \nabla_\theta J(\theta) &= \sum_{s \in \mathcal{S}} d(s) \sum_{a \in \mathcal{A}} \pi_\theta(s, a) \nabla_\theta \log \pi_\theta(s, a) \mathcal{R}_{s,a} \\ &= \mathbb{E}_{\pi_\theta} \big[ \nabla_\theta \log \pi_\theta(s, a) r \big] \end{align*} \]

  • Starts with an expectation, multiplied by a gradient, ends as an expectation

  • This remains model-free

Policy Gradient Theorem

The policy gradient theorem generalises the likelihood ratio approach to multi-step MDPs

  • Replaces instantaneous reward \(r\) with long-term value \(Q^{\pi}(s,a)\)

  • Policy gradient theorem applies to start state objective, average reward and average value objective

Policy Gradient Theorem

For any differentiable policy \(\pi_{\theta}(s,a)\),
for any of the policy objective functions \(J = J_1, J_{\text{av}R}, \text{ or } \tfrac{1}{1-\gamma} J_{\text{av}V}\),
the policy gradient is

\[ \nabla_{\theta} J(\theta) = {\color{red}{ \mathbb{E}_{\pi_{\theta}} \left[ \nabla_{\theta} \log \pi_{\theta}(s,a) \; Q^{\pi_{\theta}}(s,a) \right]}} \]

Monte-Carlo Policy Gradient (REINFORCE)

Update parameters by stochastic gradient ascent

  • Using policy gradient theorem

  • Using return \({\color{red}{v_t}}\) as an unbiased sample of \(Q^{\pi_\theta}(s_t, a_t)\)

\[ \Delta \theta_t = \alpha \nabla_\theta \log \pi_\theta(s_t, a_t) {\color{red}{v_t}} \]

function REINFORCE

    Initialise \(\theta\) arbitrarily
    for each episode \(\{s_1, a_1, r_2, \ldots, s_{T-1}, a_{T-1}, r_T\} \sim \pi_\theta\) do
        for \(t = 1\) to \(T-1\) do
            \(\theta \leftarrow \theta + \alpha \nabla_\theta \log \pi_\theta(s_t, a_t) v_t\)
        end for
    end for
    return \(\theta\)
end function

  • REINFORCE simply samples returns and adjusts parameters \(\theta\) in the direction which gets you more of those returns \(v_t\)

Puck World Example (REINFORCE)

  • Continuous actions exert small force on puck

  • Puck is regarded for getting close to target

  • Target location is reset every \(30\) seconds

  • Policy is trained using variant of Monte-Carlo policy gradient

Observations:

  • Smooth learning, however \(\cdots\)

  • Monte-Carlo Policy Gradient (REINFORCE) is slow, it takes hundreds of millions of episodes to converge

  • Variance is high

The rest of this module focuses on more efficient techniques that use same idea

Actor-Critic Policy Gradient

Reducing Variance Using a Critic

  • Monte-Carlo policy gradient still has high variance, instead of using return \(\ldots\)

  • We use a critic to estimate action-value function using a value approximator

\[ Q_\mathbf{w}(s,a) \approx Q^{\pi_\theta}(s,a) \]

Actor-critic algorithms maintain two sets of parameters, \(\textbf{w}\) and \(\theta\)

  • Critic: Updates action-value function parameters \(\mathbf{w}\)

  • Actor: Updates policy parameters \(\theta\), in the direction suggested by critic

Actor-critic algorithms follow an approximate policy gradient

\[ \nabla_\theta J(\theta) \approx \mathbb{E}_{\pi_\theta} \big[ \nabla_\theta \log \pi_\theta(s,a)\; Q_{\mathbf{w}}(s,a) \big] \]

\[ \Delta \theta = \alpha \nabla_\theta \log \pi_\theta(s,a)\; Q_{\mathbf{w}}(s,a) \]

Actor-critic combines policy gradient with value function approximation techniques

  • Replaces true value function with approximate value function (e.g. Neural network)

  • At every step, the actor moves in the direction that the critic suggests

Estimating the Action-Value Function

The critic is solving a familiar problem: policy evaluation

  • How good is policy \(\pi_{\theta}\) for current parameters \(\theta\)?

This problem was explored in previous modules, e.g. 

  • Monte-Carlo policy evaluation

  • Temporal-Difference learning

  • TD(\(\lambda\))

  • Could also use e.g. least-squares policy evaluation

Use any of these techniques to get estimate of action-value function and use that to adjust your actor

Action-Value Actor-Critic

Simple actor-critic algorithm based on an action-value critic

  • Using linear value fn approx. \(Q_{\mathbf{w}}(s,a) = \phi(s,a)^\top \mathbf{w}\)

    • Critic: Updates \(\mathbf{w}\) by linear TD(0)
    • Actor: Updates \(\theta\) by policy gradient

Function QAC

    Initialise \(s, \theta\)
    Sample \(a \sim \pi_{\theta}\)
    for each step do
        Sample reward \(r = \mathcal{R}^a_s\); sample transition \(s' \sim \mathcal{P}^a_{s,\cdot}\)
        Sample action \(a' \sim \pi_{\theta}(s',a')\)
        \(\delta = r + \gamma Q_{\mathbf{w}}(s',a') - Q_{\mathbf{w}}(s,a)\;\;\;\;\;\;\;\;{\color{red}{\text{(Critic - Value Function, Bootstraps)}}}\)
        \(\theta \leftarrow \theta + \alpha \nabla_{\theta} \log \pi_{\theta}(s,a) Q_{\mathbf{w}}(s,a)\;\;\;\;\;{\color{blue}{\text{(Actor - Update Policy Parameters)}}}\)
        \(\mathbf{w} \leftarrow \mathbf{w} + \beta \delta \phi(s,a)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\color{red}{\text{(Critic - Update parameters)}}}\)
        \(a \leftarrow a', \; s \leftarrow s'\)
    end for

Bias in Actor-Critic Algorithms

Approximating the policy gradient introduces bias

A biased policy gradient may not find the right solution

  • e.g. if \(Q_{\mathbf{w}}(s,a)\) uses aliased features, can we solve gridworld example?

Luckily, if we choose value function approximation carefully

  • Then we can avoid introducing any bias

  • i.e. We can still follow the exact policy gradient

Compatible Function Approximation Theorem

Compatible Function Approximation Theorem

If the following two conditions are satisfied:

  1. Value function approximator is compatible to the policy

\[ \nabla_{\mathbf{w}} Q_{\mathbf{w}}(s,a) = \nabla_{\theta} \log \pi_{\theta}(s,a) \]

  1. Value function parameters \(\mathbf{w}\) minimise the mean-squared error

\[ \varepsilon = \mathbb{E}_{\pi_{\theta}} \Big[ \big(Q^{\pi_{\theta}}(s,a) - Q_{\mathbf{w}}(s,a)\big)^2 \Big] \]

Then the policy gradient is exact,

\[ \nabla_{\theta} J(\theta) = \mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a)\; Q_{\mathbf{w}}(s,a) \big] \]

Proof of Compatible Function Approximation Theorem

If \(\mathbf{w}\) is chosen to minimise mean-squared error, gradient of \(\varepsilon\) w.r.t. \(\mathbf{w}\) must be zero,

\[ \begin{align*} \nabla_{\mathbf{w}} \varepsilon & = 0 \\[0pt] \mathbb{E}_{\pi_{\theta}} \Big[ \big(Q^{\pi_{\theta}}(s,a) - Q_{\mathbf{w}}(s,a)\big) \nabla_{\mathbf{w}} Q_{\mathbf{w}}(s,a) \Big] & = 0\\[0pt] \mathbb{E}_{\pi_{\theta}} \Big[ \big(Q^{\pi_{\theta}}(s,a) - Q_{\mathbf{w}}(s,a)\big) \nabla_{\theta} \log \pi_{\theta}(s,a) \Big] & = 0 \\[0pt] \mathbb{E}_{\pi_{\theta}} \Big[ Q^{\pi_{\theta}}(s,a) \nabla_{\theta} \log \pi_{\theta}(s,a) \Big] & = \mathbb{E}_{\pi_{\theta}} \Big[ Q_{\mathbf{w}}(s,a) \nabla_{\theta} \log \pi_{\theta}(s,a) \Big] \\[0pt] \end{align*} \]

So \(Q_{\mathbf{w}}(s,a)\) can be substituted directly into the policy gradient,

\[ \nabla_{\theta} J(\theta) = \mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a) Q_{\mathbf{w}}(s,a) \big] \]

Reducing Variance Using a Baseline

We subtract a baseline function \(B(s)\) from the policy gradient

  • This can reduce variance, without changing expectation

\[ \begin{align*} \mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a) B(s) \big] & = \sum_{s \in \mathcal{S}} d^{\pi_{\theta}}(s) \sum_a \nabla_{\theta} \pi_{\theta}(s,a) B(s)\\[0pt] & = \sum_{s \in \mathcal{S}} d^{\pi_{\theta}}(s) B(s) \nabla_{\theta} \sum_{a \in \mathcal{A}} \pi_{\theta}(s,a)\\[0pt] & = 0 \end{align*} \]

  • As \(B(s)\) does not rely on the action \(a\) this results in no change in expectation, so can subtract anything independent of action

  • A good baseline is the state value function \(B(s) = V^{\pi_{\theta}}(s)\)

Advantage Function

So we can rewrite the policy gradient using an advantage function, \(A^{\pi_{\theta}}(s,a)\)

\[ \begin{align*} A^{\pi_{\theta}}(s,a) & = Q^{\pi_{\theta}}(s,a) - V^{\pi_{\theta}}(s)\\[0pt] \nabla_{\theta} J(\theta) & = {\color{red}{\mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a)\; A^{\pi_{\theta}}(s,a) \big]}} \end{align*} \]

  • Tells us the advantage of choosing this action in state \(s\), compared to the average value of that state.

Estimating the Advantage Function (Option 1)

The advantage function can significantly reduce variance of policy gradient

  • So the critic should really estimate the advantage function

  • For example, by estimating both \(V^{\pi_{\theta}}(s)\) and \(Q^{\pi_{\theta}}(s,a)\)

  • Using two function approximators and two parameter vectors,

\[ \begin{align*} V_{v}(s) &\approx V^{\pi_{\theta}}(s) \\[2pt] Q_{\mathbf{w}}(s,a) &\approx Q^{\pi_{\theta}}(s,a) \\[2pt] A(s,a) &= Q_{\mathbf{w}}(s,a) - V_{v}(s) \end{align*} \]

And updating both value functions by e.g. TD learning

Estimating the Advantage Function (Easier Option 2)

For the true value function \(V^{\pi_{\theta}}(s)\), the TD error \(\delta^{\pi_{\theta}}\)

\[ \delta^{\pi_{\theta}} = r + \gamma V^{\pi_{\theta}}(s') - V^{\pi_{\theta}}(s) \]

  • this is, in turn, an unbiased estimate of the advantage function

\[ \begin{align*} \mathbb{E}_{\pi_{\theta}}[\delta^{\pi_{\theta}} \mid s,a] &= \mathbb{E}_{\pi_{\theta}}[r + \gamma V^{\pi_{\theta}}(s') \mid s,a] - V^{\pi_{\theta}}(s) \\[2pt] &= Q^{\pi_{\theta}}(s,a) - V^{\pi_{\theta}}(s) \\[2pt] &= A^{\pi_{\theta}}(s,a) \end{align*} \]

So we can in fact just use the TD error to compute the policy gradient

\[ \nabla_{\theta} J(\theta) = {\color{red}{\mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a)\; \delta^{\pi_{\theta}} \big]}} \]

In practice we can use an approximate TD error

\[ \delta_{v} = r + \gamma V_{v}(s') - V_{v}(s) \]

With the advantage that this approach only requires one set of critic parameters \(v\)

Critics at Different Time-Scales

Critic can estimate value function \(V_{v}(s)\) from many targets at different time-scales. From last module\(\ldots\)

  • For MC, the target is the return \(v_t\):

\[ \Delta v = \alpha ({\color{red}{v_t}} - V_{v}(s)) \, \phi(s) \]

  • For TD(0), the target is the TD target \(r + \gamma V(s')\):

\[ \Delta v = \alpha ({\color{red}{r + \gamma V(s')}} - V_{v}(s)) \, \phi(s) \]

  • For forward-view TD(\(\lambda\)), the target is the \(\lambda\)-return \(v_t^{\lambda}\):

\[ \Delta v = \alpha ({\color{red}{v_t^{\lambda}}} - V_{v}(s)) \, \phi(s) \]

  • For backward-view TD(\(\lambda\)), we use eligibility traces:

\[ \begin{align*} \delta_t &= r_{t+1} + \gamma V(s_{t+1}) - V(s_t) \\[2pt] e_t &= \gamma \lambda e_{t-1} + \phi(s_t) \\[2pt] \Delta \theta &= \alpha \delta_t e_t \end{align*} \]

Actors at Different Time-Scales (Same Idea)

The policy gradient can also be estimated at many time-scales

\[ \nabla_{\theta} J(\theta) = \mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a) \; {\color{red}{A^{\pi_{\theta}}(s,a)}} \big] \]

  • Monte-Carlo policy gradient uses error from complete return

\[ \Delta \theta = \alpha \big({\color{red}{v_t}} - V_{v}(s_t)\big) \nabla_{\theta} \log \pi_{\theta}(s_t, a_t) \]

  • Actor-critic policy gradient uses the one-step TD error

\[ \Delta \theta = \alpha \big({\color{red}{r + \gamma V_{v}(s_{t+1})}} - V_{v}(s_t)\big) \nabla_{\theta} \log \pi_{\theta}(s_t, a_t) \]

Policy Gradient with Eligibility Traces

Just like forward-view TD(\(\lambda\)), we can mix over time-scales

\[ \Delta \theta = \alpha \big({\color{red}{v_t^{\lambda}}} - V_{v}(s_t)\big) \nabla_{\theta} \log \pi_{\theta}(s_t,a_t) \]

  • where \(v_t^{\lambda} - V_{v}(s_t)\) is a biased estimate of the advantage function

  • Like backward-view TD(\(\lambda\)), we can also use eligibility traces

    • By equivalence with TD(\(\lambda\)), substituting \(\phi(s) = \nabla_{\theta} \log \pi_{\theta}(s,a)\):
      \[ \begin{align*} \delta &= r_{t+1} + \gamma V_{v}(s_{t+1}) - V_{v}(s_t) \\[2pt] e_{t+1} &= \lambda e_t + \nabla_{\theta} \log \pi_{\theta}(s,a) \\[2pt] \Delta \theta &= \alpha \delta e_t \end{align*} \]

This update can be applied online, to incomplete sequences

Summary of Policy Gradient Algorithms

The policy gradient has many equivalent forms

\[ \begin{align*} \nabla_{\theta} J(\theta) &= \mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a) \; v_t \big] && \text{REINFORCE} \\[2pt] &= \mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a) \; Q^{\mathbf{w}}(s,a) \big] && \text{Q Actor-Critic} \\[2pt] &= \mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a) \; A^{\mathbf{w}}(s,a) \big] && \text{Advantage Actor-Critic} \\[2pt] &= \mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a) \; \delta \big] && \text{TD Actor-Critic} \\[2pt] &= \mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a) \; \delta e \big] && \text{TD($\lambda$) Actor-Critic}\\[2pt] G_{\theta}^{-1} \nabla_{\theta} J(\theta) & = \mathbf{w} && \text{Natural Actor-Critic} \end{align*} \]

Each leads to a stochastic gradient ascent algorithm

  • Critic uses policy evaluation (e.g. MC or TD learning)
    to estimate \(Q^{\pi}(s,a)\), \(A^{\pi}(s,a)\) or \(V^{\pi}(s)\)

Natural Actor-Critic (Advanced Topic)

Alternative Policy Gradient Directions


Gradient ascent algorithms can follow any ascent direction

  • A good ascent direction can significantly speed convergence

Also, a policy can often be reparametrised without changing action probabilities

  • For example, increasing score of all actions in a softmax policy

  • The vanilla gradient is sensitive to these reparametrisations

Compatible Function Approximation (CFA)

Policy Gradient with a Learned Critic

We want to estimate the true gradient \[ \nabla_\theta J(\theta) = \mathbb{E}_\pi \!\left[ \nabla_\theta \log \pi_\theta(a|s)\, Q^\pi(s,a) \right] \]

But \(Q^\pi(s,a)\) is unknown — so we approximate it with a parametric critic \({\color{red}{Q_w(s,a)}}\)

Compatibility Conditions for Critic

  1. Linear in the policy’s score function \[ Q_w(s,a) = w^\top \nabla_\theta \log \pi_\theta(a|s) \]

  2. Weights chosen to minimise on-policy error \[ w^* = \arg\min_w \mathbb{E}_\pi \left[ \big(Q^\pi(s,a) - Q_w(s,a)\big)^2 \right] \]

Compatibility Conditions—A Beautiful Result

If both compatibility conditions hold, then

\[ \nabla_\theta J(\theta) = \mathbb{E}_\pi \left[ \nabla_\theta \log \pi_\theta(a|s)\, Q_w(s,a) \right] \]

That is — the approximate critic yields the exact policy gradient.

Intuition

  • The critic lies in the same space as the policy’s gradient features

  • The actor and critic share a common geometry

  • The critic projects \(Q^\pi\) onto the policy’s tangent space

  • Variance reduction without bias — a perfect harmony between learning and estimation

Natural Policy Gradient—Fisher Information Matrix

The natural policy gradient is parametrisation independent

  • It finds the ascent direction that is closest to the vanilla gradient, when changing policy by a small, fixed amount

\[ \nabla^{\text{nat}}_{\theta} \pi_{\theta}(s,a) = G_{\theta}^{-1} \nabla_{\theta} \pi_{\theta}(s,a) \]

  • where \(G_{\theta}\) is the Fisher information matrix (Measures how sensitive a probability distribution is to changes in its parameters) \[ G_{\theta} = \mathbb{E}_{\pi_{\theta}} \Big[ {\color{blue}{\nabla_{\theta} \log \pi_{\theta}(s,a) \; \nabla_{\theta} \log \pi_{\theta}(s,a)^\top }}\Big] \]

Natural Actor-Critic—Compatible Function Approximation

Uses compatible function approximation,

\[ \nabla_{\mathbf{w}} A_{\mathbf{w}}(s,a) = \nabla_{\theta} \log \pi_{\theta}(s,a) \]

So the natural policy gradient simplifies,

\[ \begin{align*} \nabla_{\theta} J(\theta) &= \mathbb{E}_{\pi_{\theta}} \big[ \nabla_{\theta} \log \pi_{\theta}(s,a) \; A^{\pi_{\theta}}(s,a) \big] \\[2pt] &= \mathbb{E}_{\pi_{\theta}} \Big[ \nabla_{\theta} \log \pi_{theta}(s,a) \, \nabla_{\theta} \log \pi_{\theta}(s,a)^\top \Big] \mathbf{w} \\[2pt] &= G_{\theta} \, \mathbf{w}\\[2pt] {\color{red}{\nabla_{\theta}^{\text{nat}} J(\theta)}} & {\color{red}{= \mathbf{w}}} \end{align*} \]

i.e. update actor parameters in direction of critic parameters \(\mathbf{w}\)

Natural Policy Gradient—Parameterisation Invariant

  • The black contours show level sets of equal performance \(J(\theta)\)
  • The blue arrows show the ordinary gradient ascent direction for each point in parameter space (not orthogonal to the contours, behave irregularly across space)
  • The red arrows are the natural gradient directions (ascent directions are orthogonal to contours and smoothly distributed)
  • Natural gradient respects geometry of probability distributions—it finds steepest ascent direction measured in policy (distributional) space, not raw parameter space

Natural Actor Critic in Snake Domain

  • The dynamics are nonlinear and continuous—a good test of policy gradient methods.

Natural Actor Critic in Snake Domain (2)

  • The geometry of the corridor causes simple gradient updates to oscillate or diverge, but natural gradients (which adapt to curvature via the Fisher matrix independent of parameters) make stable, efficient progress.

Proximal Policy Optimisation (PPO) (Advanced Topic)

Proximal Policy Optimisation (PPO)


Goal: Stable, sample-efficient policy improvement

Idea: Constrain how far the new policy moves from the old one at each update during actor-critic cycle

Policy Objective Functions (Revisited)

From a policy gradient perspective, the true objective function \(J^{{\pi}_{\theta}}(\theta)\) over policy \(\pi_{\theta}\) is defined as follows

\[ J^{{\pi}_{\theta}}(\theta) = \mathbb{E}_{\tau \sim \pi_{\theta}} [G_0]=V^{\pi \theta}(d_0) \]

where \(d_0\) is the distribution over initial states at the start of each episode \(\tau\)

However, there are two problems in the actor-critic setting:

1. Computing \(J^{{\pi}_{\theta}}(\theta)\) exactly would require integrating over all trajectories, \(\tau\), of the current policy, which is impractical

2. If we update the parameters \(\theta\), it will effect objective value during the optimisation process, leading to (circular) feedback

We therefore need a surrogate objective independent of the trajectory distribution under the new policy \(\color{blue}{\pi_{\theta}}\) we are building

Surrogate Objective

From the policy-gradient theorem, we can define the importance ratio

\[ r_t(\theta) \;=\; \frac{\pi_\theta(a_t\mid s_t)}{\pi_{\theta_{\text{old}}}(a_t\mid s_t)} \qquad \]

We now define the surrogate objective \(L_{PG}\) for the true objective

\[ L_{PG}(\theta) \;=\; \mathbb{E}_t\!\big[\, r_t(\theta)\,\hat A_t \,\big] \]

  • Where \(\hat{A}_t\) captures how much better action \(a_t\) was than the state’s average

  • \(\hat{A}_t\) is an estimator of the true advantage function \(A^{\pi}\)

  • \(A^{\pi}(s_t,a_t) = Q^{\pi}(s_t, a_t) - V^{\pi}(S_t)\)

Clipped Surrogate (Core Idea)

Kullback-Leibler (KL) divergence theory tells us we want improvement without overly large steps in policy space, so we define

\[ L^{\text{CLIP}}(\theta) \;=\; \mathbb{E}_t\! \left[ \min\!\Big( r_t(\theta)\,\hat A_t,\; \mathrm{clip}\!\big(r_t(\theta),\,1-\epsilon,\,1+\epsilon\big)\,\hat A_t \Big) \right] \]

  • If \(r_t(\theta)\) leaves the interval \([1-\epsilon,\,1+\epsilon]\), the objective is clipped.

  • Typical range for \(\epsilon \in [0.1,\,0.2]\).

  • Prevents destructive updates while preserving ascent direction

The clipped surrogate objective in PPO plays a similar stabilising role to compatible function approximation — both constrain policy updates so that gradient estimates remain accurate and unbiased with respect to the true policy improvement direction.

Complete PPO loss

\[ L^{\text{PPO}}(\theta) = \mathbb{E}_t\!\Big[{\color{blue}{L^{\text{CLIP}}(\theta)}} - c_1\,{\color{red}{\big(V_\theta(s_t)-V_t^{\text{target}}\big)^2}} + c_2\,\mathcal{H}\!\left[\pi_\theta(\cdot\mid s_t)\right] \Big] \] \(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\)where \(c_1, c_2\) are coefficients

The actors policy gradient (surrogate objective) is \(\color{blue}{L^{CLIP}(\theta)}\)

  • This encourages the policy to increase the probability of actions with positive advantage and decrease it for negative ones

The critics value function is \(\color{red}{\big(V_\theta(s_t)-V_t^{\text{target}}\big)^2}\)

  • This trains the network to predict correct returns (mean-squared error).

The entropy bonus \(\mathcal{H}\) encourages exploration

\[ \mathcal{H}\big[\pi_\theta(\cdot \mid s_t)\big] = - \sum_{a} \pi_\theta(a \mid s_t) \log \pi_\theta(a \mid s_t) \]

The entropy term encourages exploration by rewarding stochastic (uncertain) policies.

  • It’s high when the policy is uncertain or “spread out” (exploratory).

  • It’s low when the policy is confident or deterministic.

  • The dot “\(\cdot\)” in \(\pi_{\theta}(\cdot | s_t)\) means over all possible actions, i.e. the vector of probabilities  \(\pi_{\theta}(a_1,s_t), \pi_{\theta}(a_2,s_t), \ldots\)

In practice this maintains stochasticity until policy becomes more confident or deterministic

Generalised Advantage Estimation (GAE)

In practice, PPO uses a low-variance, low-bias estimate of the advantage \(A^\pi(s_t,a_t)\).

TD error: \[ \delta_t \;=\; r_t + \gamma\,V_\phi(s_{t+1}) - V_\phi(s_t) \]

GAE-\(\lambda\): \[ \hat A_t^{(\lambda)} \;=\; \sum_{l=0}^{\infty} (\gamma\lambda)^l\,\delta_{t+l} \;=\; \delta_t + \gamma\lambda\,\delta_{t+1} + (\gamma\lambda)^2\,\delta_{t+2} + \cdots \]

Return/target used for critic \[ \hat V_t^{\text{target}} \;=\; \hat A_t^{(\lambda)} + V_\phi(s_t) \]

  • \(\lambda\in[0,1]\) trades bias \(\leftrightarrow\) variance, typical PPO: \(\gamma \approx 0.99\), \(\lambda \approx 0.95\).

PPO Algorithm

PPO Algorithm

Repeat

\(\;\;\;\) Collect trajectories with \(\pi_{\theta_{\text{old}}}\)

\(\;\;\;\) Compute returns and advantages using GAE-\(\lambda\)

\(\;\;\;\) Optimise \(L^{\text{CLIP}}\) for \(K\) epochs over mini-batches

\(\;\;\;\) Update old params: \(\theta_{\text{old}} \leftarrow \theta\)

Until a stop condition holds (e.g., total timesteps \(\geq T\), or moving-average return \(\geq R_{\text{target}}\), or max iterations reached)

  • Multiple epochs over the same batch are okay because clipping limits drift

Why PPO works (intuition)

First-order solution method

  • No additional constraint solving required which can introduce second-order effects

Trust-region-like behaviour via clipping

  • Optimisation within trust-region involves only taking steps that stay within a region where local approximation is reliable (founded on KL information theory)

Robust across discrete/continuous control

  • Strong baseline performance in practice

PPO Fine tuning ChatGPT & human feedback (Revisited)

  • Proximal policy optimisation (PPO) is used by ChatGPT 3.5

PPO in Agentic AI, Robotics & World Models

PPO is becoming popular again for Agentic AI modes, and is used in

  • Chat GPT’s Operator, and

  • Claude’s Computer Use modes

PPO is also becoming popular for World Models in robotics, and is used in

  • Vision, Language & Action (VSA) attention-based transformers

Recent Policy Optimisation Techniques

ChatGPT4 uses Direct Preference Optimisation (DPO)

DeepSeek’s R1 uses Group Relative Policy Optimization (GRPO)